블로그를 참고해서 풀었는데 누구 블로그를 참고했는지 기억이 나지 않는다ㅠㅠㅠ
https://www.acmicpc.net/problem/5639
5639번: 이진 검색 트리
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다
www.acmicpc.net
먼저 본 문제에서는 두가지 눈여겨봐야할 포인트들이 있다.
1. 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
2. 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
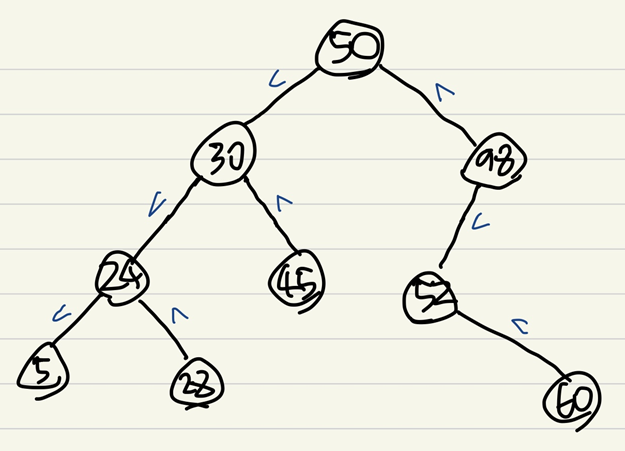
말그대로 파란색으로 크기를 표시해둔걸 봤을 때, 한 노드의 왼쪽에는 무조건 더 작은 숫자가, 오른쪽에는 무조건 더 큰 숫자가 온다는 의미이다.
이와 같은 이진트리의 전위순회가 주어졌을 때 후위순회를 출력해야하는 문제이다.
재귀로 푸는 방식도 있었지만 이해가 가지 않았기 때문에 트리를 직접 구성해서 푸는 방식을 공부했다.
트리의 구성
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Tree:
def __init__(self, value): #한 노드의 초기 left와 right는 None으로, value는 자기 자신으로
self.left = None
self.right = None
self.value = value
def insertion(self, value):
if value < self.value:
if self.left is None:
self.left = Tree(value)
else:
self.left.insertion(value)
else:
if self.right is None:
self.right = Tree(value)
else:
self.right.insertion(value)
def postorder(self):
if self.left is not None:
self.left.postorder()
if self.right is not None:
self.right.postorder()
print(self.value)
|
cs |
postorder 함수는 나중에 설명하고 Tree 클래스의 생성자인 __init__와 insertion부터 설명하도록 하겠다.
(자고로 파이썬에서 클래스의 생성자를 만들 때에는 __init__을 사용한다.)
트리의 생성자
|
1
2
3
4
5
|
class Tree:
def __init__(self, value): #한 노드의 초기 left와 right는 None으로, value는 자기 자신으로
self.left = None
self.right = None
self.value = value
|
cs |

생성자를 부르는 순간 하나의 노드가 생성되는 것이고 위와 같은 상황에서는 value가 50일 때 self.value에는 value고 왼쪽과 오른쪽에는 아무것도 없는 상태여서 None을 넣어준 것이다.
새 노드의 삽입
|
1
2
3
4
5
6
7
8
9
10
11
|
def insertion(self, value):
if value < self.value:
if self.left is None:
self.left = Tree(value)
else:
self.left.insertion(value)
else:
if self.right is None:
self.right = Tree(value)
else:
self.right.insertion(value)
|
cs |
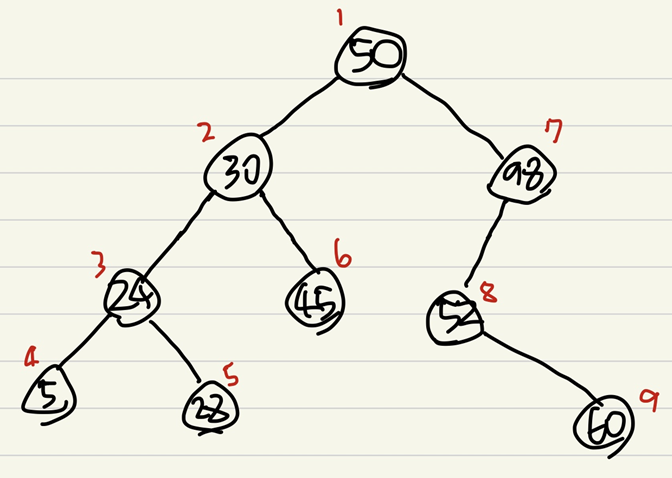
트리의 전위순회라는것은 위 그림처럼 왼쪽부터 다 방문하면서 출력한 뒤에 오른쪽을 방문하는 형태를 말한다. 앞서 이야기한 포인트들과 전위순회를 이용해서 트리를 구성해내는 것이 가능하다.

예를들어서 위와 같은 트리의 상태에서 45를 넣는다고 하면 45는 50보다 작기 때문에 왼쪽에 들어가야하지만 왼쪽에는 이미 30이 있기 때문에 self.left.insertion(value)로 왼쪽 노드에 대한 insertion 함수를 호출한다.

다음으로 30 노드에서 비교해보면 45는 30보다 크다. 그리고 30의 오른쪽에는 노드가 없다.

최종적으로 형성된 트리의 모습이다. 전위순회 순서로 입력을 받기 때문에 해당 방법으로 트리를 구성하는 것이 가능하다.
후위순회 출력
|
1
2
3
4
5
6
|
def postorder(self):
if self.left is not None:
self.left.postorder()
if self.right is not None:
self.right.postorder()
print(self.value)
|
cs |
후위순회는 흔히 알고있는 방식대로 print를 재귀의 마지막 부분에 써주면 된다.
(참고: 전위순회 - print가 제일 위로 간다. 중위순회 - print가 중간에 있다.)
'프로그래머스 풀이' 카테고리의 다른 글
| 프로그래머스 2단계 - n^2 배열자르기 (Python) (0) | 2022.03.11 |
|---|---|
| 프로그래머스 2단계 - [1차] 캐시 (0) | 2022.02.13 |
| 프로그래머스 2단계 - 모음사전 (Python) (2) | 2022.01.28 |
| 프로그래머스 2단계 - 후보키 (Python) (0) | 2021.12.01 |
| 프로그래머스 2단계 - 괄호 회전하기 (Python) (0) | 2021.11.17 |
