깃허브:
github.com/MSIQOC/BOJ/blob/master/b9095_123%EB%8D%94%ED%95%98%EA%B8%B0.java
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net


간단하게 숫자가 주어지면 주어진 숫자를 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 문제이고, 처음엔 생각해내는 것이 어려울 수 있어도 잘 생각해보면 다이나믹프로그래밍으로 쉽게 풀리는 문제이다.

표현하는데에 사용되는 숫자인 1, 2, 3을 1과 2와 3의 합으로 표현하는 경우의 수는 다음과 같다. 여기에서 4를 표현할려면 어떻게 해야할까?
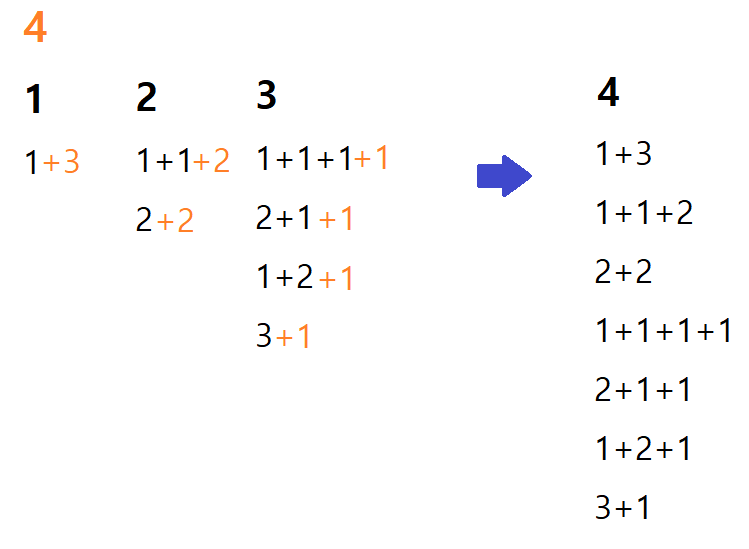
1에 3을, 2에 2를, 그리고 3에 1을 더해서 4를 만들 수 있다. 즉, 4를 1, 2, 3의 합으로 만들 수 있는 모든 경우의 수는 1의 경우의 수 + 2의 경우의 수 + 3의 경우의 수가 된다. 여기에서 숫자 i의 경우의 수를 D[i]로 나타낸다면, D[4] = D[3] + D[2] + D[1]이 되는 것이다.

5도 마찬가지로 풀 수 있다. 이전에 이미 1,2,3의 합으로 이루어진 경우의 수들을 다 구해둔 상태이고 5는 2에 3을, 3에 2를, 그리고 4에 1을 더해서 만들 수 있다. 한마디로 5의 경우의 수는 2, 3, 4의 경우의 수를 합친 것으로 나타낼 수 있고, 이를 식으로 표현하면 D[5] = D[4] + D[3] + D[2]로 표현할 수 있다.
여기에서 패턴을 찾아서 점화식으로 나타낼 수 있고, 그 점화식은 D[i] = D[i-1] + D[i-2] + D[i-3]이 된다. 코드로 나타내면 D[1], D[2], D[3]까지는 미리 써놓고 D[4]부터 구해둔 것들을 사용해서 구하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import java.io.*;
public class b9095_123더하기 {
public static void main(String []args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); //값읽기
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
int D[] = new int[12];
D[1] = 1;
D[2] = 2;
D[3] = 4;
for(int i=4; i<=11; ++i) {
D[i] = D[i-1]+D[i-2]+D[i-3];
}
while(n-->0) {
int in = Integer.parseInt(br.readLine());
bw.write(D[in]+"\n");
}
bw.flush();
}
}
|
'백준 풀이' 카테고리의 다른 글
| 백준 15990 - 1, 2, 3 더하기 5 (0) | 2021.02.07 |
|---|---|
| 백준 11025 - 카드 구매하기 (0) | 2021.02.07 |
| 백준 17299 - 오등큰수 (0) | 2021.02.05 |
| 백준 1158 - 요세푸스 문제 (0) | 2021.01.10 |
| 백준 9012 - 괄호 (0) | 2021.01.10 |



