참고 블로그:
백준 17299번 오등큰수 문제 스택 활용 풀이 ( Java )
17299번: 오등큰수 첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다. www.acmicpc.net 1 2 3 4 5 6 7 8 9 10 11 12 13..
takeknowledge.tistory.com
17299번: 오등큰수
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.
www.acmicpc.net

풀다가 못풀어서 결국 티스토리 블로그를 참고해서 풀었지만, 코드에 대한 설명이 필요할 것 같아서 글로 남기려고 한다. 문제를 이해하는 데에도 나에게 있어서 상당히 많은 시간이 걸렸는데, 문제의 예제 입력 1을 예로 들어서 설명을 해보도록 하겠다.
문제 설명:

문제에서 제시된 대로라면 F(x)는 x가 전체에서 등장한 횟수이고, 각 숫자 x마다 등장한 횟수 F(x)를 밑에 적어주었다. 1은 세번 등장하니 3으로, 2는 두번 등장해서 2로, 그리고 3과 4는 전체에서 한번밖에 등장을 안하기 때문에 1로 적어주었다.
오등큰수의 개념을 설명하기 위해서 왼쪽에서 네번째 숫자인 3을 예로 들어보면, 네번째보다 오른쪽에 위치하면서 F(x)가

오등큰수란, F(x)가 지정된 숫자의 F(x)보다 크고 해당 숫자의 오른쪽에 위치하면서 제일 처음으로 등장하는 숫자다. 글로의 설명이 어려우니 예시로 그림에서처럼 지정된 숫자를 왼쪽에서 네번째 숫자인 3으로 정한다면, 3보다 오른쪽에 위치하면서 3의 F(x)인 1보다 큰 F(x)를 가지는 수는 끝에 두 숫자, 즉 2와 1이 된다. (두 숫자의 F(x)는 각각 2와 3으로 둘 다 3의 F(x)인 1보다 크다.) 하지만 오등큰수의 조건에서는 "제일 처음으로 등장하는" 숫자라는 것이 있기 때문에 네번째 숫자의 오등큰수는 왼쪽에서 6번째 숫자인 2가 된다.

숫자 1과 같은 경우에는 F(x)가 3인데, 1보다 오른쪽에 위치하면서 F(x)가 3보다 큰 숫자는 존재하지 않기 때문에 숫자 1의 오등큰수는 -1이 된다.
이와 같은 방법으로 오등큰수를 찾을 수 있고, 이는 스택의 성질을 활용해서 풀어낼 수 있다.
코드와 스택을 이용한 풀이 설명:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
import java.io.*;
import java.util.*;
public class ba17299_오등큰수 {
public static void main(String[] args) throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out)); //값출력
Scanner sc = new Scanner(System.in);
Stack<Integer> stack = new Stack<>();
int n = sc.nextInt();
long a[] = new long[1000001];
int index[] = new int[1000001];
long ans[] = new long[1000001];
for(int i=0; i<n; ++i) {
int m = sc.nextInt();
++a[m];
index[i] = m;
}
//gilog은 다음 빈칸을 가리킴
//index의 사이즈는 gilog-1
stack.push(0);
for(int i=1; i<n; ++i) {
if(stack.empty()) {
stack.push(i);
}
while(!stack.empty() && a[index[i]]>a[index[stack.peek()]]) {
int aa = stack.pop();
ans[aa] = index[i];
}
stack.push(i);
}
if(!stack.empty()) {
while(!stack.empty())
ans[stack.pop()] = -1;
}
for(int i=0; i<n; ++i)
bw.write(ans[i] + " ");
//a[0] = 10;
bw.flush();
}
}
|

총 7개의 숫자가 있기 때문에 index 0부터 6까지 하나하나 조건을 따져가며 스택에 넣었다가 빼게 된다. (스택에는 숫자 x를 넣지 않고 해당 숫자의 인덱스를 넣는다.) 만약 다음에 넣을 인덱스를 가진 숫자의 F(x)가 가장 최근에 스택에 들어갔던 인덱스를 가진 숫자의 F(x)보다 작거나 같으면 스택에서 어떤 것도 빼지 않고 계속해서 스택에 다음 인덱스를 넣게 된다.

만약 다음에 들어갈 숫자의 F(x)가 최근에 스택에 들어간 숫자의 F(x)보다 더 큰 상황이 발생했을 경우, 그동안 스택에 쌓여왔던 인덱스들 중 다음에 들어갈 인덱스를 가진 숫자의 F(x) 보다 작은 F(x)를 가진 수들은 오등큰수를 찾았다고 할 수 있다. (위치가 더 오른쪽에 있으면서 처음으로 자기자신보다 큰 F(x)가 등장하기 때문에)
위 그림에서는 3번과 4번 인덱스를 가진 수(3과 4)의 오등큰수가 5번 인덱스를 가진 수인 2가 된다.

5번을 스택에 넣은 후 6번도 마찬가지로 F(x)가 스택의 가장 위에 있는 5번의 F(x)보다 크다. 이렇게 될 경우 인덱스 5번과 2번을 가진 수들의 오등큰수는 인덱스 6번인 숫자 1이 된다.
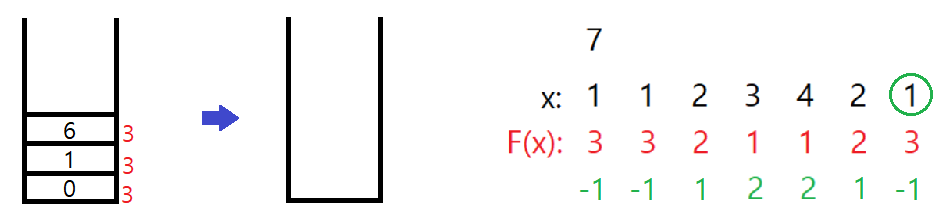
마지막으로 모든 인덱스를 다 스택에 집어넣은 후에 스택이 비지 않을 경우에는 오등큰수가 -1인걸로 표시할 수 있다.
'백준 풀이' 카테고리의 다른 글
| 백준 11025 - 카드 구매하기 (0) | 2021.02.07 |
|---|---|
| 백준 9095 - 1, 2, 3 더하기 (다이나믹 프로그래밍) (0) | 2021.02.05 |
| 백준 1158 - 요세푸스 문제 (0) | 2021.01.10 |
| 백준 9012 - 괄호 (0) | 2021.01.10 |
| 백준 17413 - 단어뒤집기 2 (0) | 2021.01.09 |



